RCE junk
2012-02-08
Shmoocon 2012 "Blocky" (RE 400) Write-Up

2011-04-06
Shmoocon 2011 Crypto Pack Solved! And Pairings And SAGE!

Not long after Dcoder's solve, user ged_ posted valid serials for his name, but sadly never supplied an explanation of his methods.
Like stated previously, the choice of python and the simplicity of the first few challenges were intended to entice contenders into actually doing the challenges. The 4'th and 5'th challenge were to inject some new material into the keygenme problem space and that's what I'll discuss here.
Challenge 4 is a large rational function calculating the "multiply-by-m" map of a point on an elliptic curve. Formulas exist to add and double points, so it's sensible that they may be composed to derive formulas for multiplication by a given coefficient. This is just a giant formula for multiplying by 13. No way could you take care of the algebra by hand: I used SAGE's EllipticCurve function multiplication_by_m() which Dcoder independently used when he suggests recreating the map for verification. A guessing game wasn't intended: the degree of the polynomial being 169 (132) is a clue. Blackboxing the function is even feasible.
Challenge 5 is the BLS short signature scheme using pairings on elliptic curves. Pairings are freaking magic and here I'll try to explain why. We'll have the typical mapping from an elliptic curve group (where the group operation is written as addition and thus repeated operations are written as multiplication) to the multiplicative group of an extension field (where repeated operations are written as exponentiation). Thus we write the bilinear property as:
e(aP, bQ) = e(P,Q)ab
So the map doesn't care if you first multiply the points and then ask for output, or if you ask for the output and then exponentiate the result. Why is a mapping with this property useful?
Recall the computational DH problem (CDH) by thinking of the eavesdropper's perspective of an DH key exchange. Eve views P, aP, and bP, but cannot compute the shared secret abP. But if Eve were handed the shared secret among a thousand other random group elements, could she discern abP from the decoys? This is called the decision DH problem (DDH) and is solvable if the group is equipped with a pairing. How? Given (P, aP, bP, abP) Eve tests e(P, abP) = e(aP, bP) = e(P,P)ab.
Now look at it from a public-key standpoint. Suppose I publish E=<G>, xG but keep x secret. You could challenge my claim of knowing x by asking me to multiply it on a new point P. I'd return xP, just not x. You'd then have (G, xG, P, xP) and could verify e(G, xP) = e(xG, P) = e(G,P)x.
If this isn't magic enough, think now how you can operate on e(G,P)x without knowing x. The pairing kind of exposes the x for involvement in future computations without explicitly revealing its value. Three-party key agreement is the clearest use of this property. When the three parties {A,B,C} compute respectively {e(bG,cG)a, e(aG,cG)b, e(aG,bG)c}, everybody arrives at e(G,G)abc, yet each party knows only the value of their own {a,b,c}.
The BLS signature scheme is is exactly the same as the first example with DDH above, except that the challenge point P is the message mapped to a point, and the xP is renamed the signature S. Verifying the signature is verifying the tuple (G, xG, P, S).
There are a few pairings now, but the Weil pairing is seemed like the "hello world" of pairings and still it was very difficult to get working. I owe mostly to Ben Lynn for writing his thesis in a clear, explanatory fashion and not being too "math leet" to include worked examples. Also, I had a bug when evaluating points on lines that went through infinity and couldn't have figured it out without David Hanson's Weil pairing implementation in SAGE.
Producing curve parameters is an entirely separate problem. The paper on BN (Barreto, Naehrig) curves had an algorithm that wasn't too difficult to type out and test. Here's the implementation in SAGE. Finally crypto5 can be constructed:
sage: [E,g1] = search_embed_12(64)As expected from the BN curve algorithm, we have a prime order curve. This means that r=#E and every point is in the r-torsion E[r]. This r-torsion's definition is a subgroup whose elements' orders divide r, but here every elements' order is exactly r. Call this group by a new name G1 = <g1> to detach it from E since we'll be moving E over larger fields.
Elliptic Curve defined by y^2 = x^3 + 13 over Finite Field of size 9524793152874449521
(1 : 4577206343548535956 : 1)
sage: r = E.order()
sage: is_prime(r)
True
Over increasingly extended fields, #E grows, fast. Not until extension 12 (the embedding degree) does the group E(Fp12) contain E[r2].
sage: E=EllipticCurve(GF(9524793152874449521^12,'a'),[0,0,0,0,13])That's a lot of points! E[r2] is the direct product of G1 and some other r-sized subgroup in E we'll call G2. To find G2, we take a random point and multiply by #E/r2.
sage: E.order()
557527939388338455999335177184553128648411435525495183120877629267756649506692825601416365268161565197227820626524244139422343537066988585815195692298420149498809296111861768128843274828063908967761768686256781963953791177011200
sage: g2=E.random_point() * Integer(E.order()/r^2)We see that g2 is not in G1 and its order is the prime r so G2 = <g2>. Now, g1 and g2 together form a sort of basis by which all of E[r2] can be generated; every element in E[r2] can be written as a*g1 + b*g2 where a,b from Zr.
sage: g2.order()
9524793149788155121
sage: g2
(28930072329430674*a^11 + 3476916985694553167*a^10 + 7416446501236864153*a^9 + 1546806533803993509*a^8 + 9258625410126221791*a^7 + 3946459769382694037*a^6 + 9082757750092742366*a^5 + 4925994372571715422*a^4 + 9356115311475410715*a^3 + 3239246275650681784*a^2 + 2530023797852594208*a + 2582477270547956977 : 4569041207989982512*a^11 + 392122047555439583*a^10 + 53398003196643395*a^9 + 2471082114350274565*a^8 + 3769727620341931341*a^7 + 2253879482993753613*a^6 + 7323759157123465679*a^5 + 1956558743620835276*a^4 + 1065433853209237195*a^3 + 8009494946720473686*a^2 + 8874621118513866374*a + 544373368025887171 : 1)
We'll have the pairing map G1 x G2 -> Fp12. The input groups must be different, otherwise the points will be linearly dependent and the pairing will become degenerate. G1's members' coordinates have a nice compact representation of a single ground field element while each of G2's members's coordinates require 12 ground field elements. The public key P should then live in G2 while the signature S lives in G1. Choose private key x and compute:
sage: x = 1223334444333221111To convert a message (the user name input to the crackme) to a point in G1, we just convert the name to a number and multiply generator g1. Suppose the name converts to 123456, then the signature is simply:
sage: P = g2*x
sage: P
(9234041514029458289*a^11 + 7779915664763212307*a^10 + 6346523241154805362*a^9 + 5513000999900352828*a^8 + 7183243026634094341*a^7 + 6887819078187130363*a^6 + 5522347192587339249*a^5 + 832499822664426562*a^4 + 1305341026780126317*a^3 + 5936146128578535690*a^2 + 474243480778556212*a + 6400173802196845754 : 4965553112357672903*a^11 + 3816268899954016796*a^10 + 359467867455554913*a^9 + 212427926173001815*a^8 + 5152204995298522178*a^7 + 915090504523216963*a^6 + 8111126461946895687*a^5 + 318194623178172360*a^4 + 8053089739653482422*a^3 + 171210160812342620*a^2 + 6985863117841018225*a + 122495515023342804 : 1)
sage: M = 123456*g1You can store just one of the coordinates and a bit to distinguish candidate roots when solving the other coordinate. Despite sections in the BN paper specifically aimed at helping the reader compress points by solving cube roots, I failed to understand and implement this in time and the crackme had to be supplied with both coordinates :( You can hardly call this a short signature. Anyways, verifying the signature now is verifying the DH tuple (g2, P, M, S) = (g2, x*g2, 123456g1, 123456x*g1). We compare e(x*g2, M) with e(g2, 123456x*g1) and hopefully get e(g2,g1)123456x:
sage: M
(5525487180627916384 : 8968938521026939071 : 1)
sage: S = x*M
sage: S
(7298443986699715260 : 507887173084537875 : 1)
sage: g2.weil_pairing(S,r)All the same result! Sanity check passed! Here's an attempt to diagram the entire process. Please don't trust this for correctness:
3636921704439622827*a^11 + 7161351127997094877*a^10 + 7731397384313800342*a^9 + 2976376815617375612*a^8 + 6846986400478961310*a^7 + 7580008168259595715*a^6 + 715697510382978485*a^5 + 5707351599709597252*a^4 + 7748158347504684570*a^3 + 9039946616134562331*a^2 + 2408156042808436778*a + 72829371319520371
sage: P.weil_pairing(M,r)
3636921704439622827*a^11 + 7161351127997094877*a^10 + 7731397384313800342*a^9 + 2976376815617375612*a^8 + 6846986400478961310*a^7 + 7580008168259595715*a^6 + 715697510382978485*a^5 + 5707351599709597252*a^4 + 7748158347504684570*a^3 + 9039946616134562331*a^2 + 2408156042808436778*a + 72829371319520371
sage: g2.weil_pairing(g1,r) ^ (123456*x)
3636921704439622827*a^11 + 7161351127997094877*a^10 + 7731397384313800342*a^9 + 2976376815617375612*a^8 + 6846986400478961310*a^7 + 7580008168259595715*a^6 + 715697510382978485*a^5 + 5707351599709597252*a^4 + 7748158347504684570*a^3 + 9039946616134562331*a^2 + 2408156042808436778*a + 72829371319520371

[HBK]'s "Indiana Jones and the Wizard of Oz"
[difficulty: 2][protection: Stone Temple Puzzle]

[HBK]'s first submissions is a fun and creative crackme. Don't let the difficulty fool you! "...to gain access to the cave, all the letter 'tablets' must be 'pushed' hmm.. no problem for indiana !!!" :)
http://crackmes.de/users/hbk/indiana_jones_si_vrajitorul_din_oz/2011-03-16
Wireshark as 010 Editor Alternative?
Why couldn't Wireshark's packet dissection capabilities be used as an open-source alternative to 010 Editor's binary template feature?
Pros:
- free, open source
- C > 010's BT language
- python support?
- much harder to write
- no editor, just viewer
- extra preparation step
- bugs
 pcap-wrap.c - wrap files in pcap capture format
pcap-wrap.c - wrap files in pcap capture formatMuch code can be generated (will show in a future blog post) and in fact, some of the example plugins shown from epan/dissectors/* are generated. See packet-rrc.c which weights in at over 7MB! Anyways, as a proof of concept, I made a dissector for the canonical WAV file format.
 packet-wav.c - dissector for canonical WAV files
packet-wav.c - dissector for canonical WAV filesNearly every rule in the coding style / compatibility section was broken in this code and there's probably leaks and security problems; just a disclaimer. So what does it look like?

Now can we simplify things? If we forfeit the ability to do the advanced filter expressions, we can declare just one "dummy" field and subtree, and use its handle every time we add a field and subtree. Instead of relying on Wireshark to format the data for us (and using its complicated string lookup and bitfield mechanisms), we add most things with field type FT_NONE and with *_format() functions, supplying our own strings. Often you can just tack on additional data to an item via proto_item_append_text(). Here's take two:
 packet-wav-new.c - a clearer dissector for canonical WAV files
packet-wav-new.c - a clearer dissector for canonical WAV filesA WAV file is almost a disappointing example, but again it was just for POC. Here's Wireshark chewing on something a little more complicated:

wireshark/epan/packet.c: call_dissector_work() (returns 0)
wireshark/epan/packet.c: dissector_try_port_new() (returns FALSE)
wireshark/epan/packet.c: dissector_try_port() (returns FALSE)
wireshark/epan/dissectors/packet-frame.c: dissect_frame() (doesn't try other dissectors in sub_dissectors)
I don't have the wireshark know-how to make a proper fix/patch and Wireshark bug database is down at the moment. It sucks but for now I make sure just one of these plugins are present to wireshark at a time.
2011-02-15
Waganono's "Root Me #1"

Waganono appears to be back! After solving CHAAK's maze crackme "Keygenme #1" earlier this month, he's submitted a new keygenme. It's not too hard and not too easy! Check it out!
2011-02-02
Shmoocon 2011 Crypto Challenge Pack

The Ghost In The Shellcode organizers gave me the privilege again this year to write some challenges for their CTF event. Here are the contents of the README:
Shmoocon 2011 Cryptography Challenge Pack
-------------------------------------------------------------------------------
http://www.ghostintheshellcode.com/
https://www.shmoocon.org/ghost_in_the_shellcode
-------------------------------------------------------------------------------
These are the cryptography challenges submitted to the Shmoocon 2011 "Ghost In
The Shellcode" organizers for potential use in the CTF event and December
qualifier.
-------------------------------------------------------------------------------
Challenges were made with a few features to facilitate analysis:
1) open source (skip the disassembly->algorithm translation phase)
2) calculations, input, output are all in decimal, allowing easy entry of
values between external tools
-------------------------------------------------------------------------------
Python?
1) seems program logic is easy to understand even without knowing Python
2) debugger is easy to use (python -mpdb chall1.py) but you probably won't need
it
3) installs nearly everywhere
4) tested with 2.6.5
-------------------------------------------------------------------------------
I hope you find these algorithms easy to understand, interesting, but
challenging to keygen. Chall4 and Chall5 are exceptions :)
http://crackmes.de/users/andrewl.us/shmoocon_2011_crypto_challenge_pack/
2011-01-10
2011 Shmoocon CTF Warmup Results
Unfortunately the crypto one fell faster than I expected and ended up being the easiest challenge of the three! LarsH and kaliman submitted a solution in just 28 minutes! From the chat, I gathered that people solved it in three ways:
- typing the equations into wolfram alpha (this tool is becoming very popular! see recent solutions by tamaroth at crackmes.de among others)
- using the Chinese remainder theorem (intended method)
- using the method of successive substitution
I've never seen the third method until now! Can there exist systems where CRT fails but this method finds a solution?
The third challenge ended up being really really interesting and apparently the hardest. Awesie, the only solver and winner of the warmup and Shmoocon barcode, graciously details his methods for the public: http://ppp.cylab.cmu.edu/wordpress/?p=410. Congratulations awesie!
2010-10-22
One Hell of an Anti-Debug! HideFromDebugger
Since my breakpoints were at User32's WaitMessageWhatever return, this would happen if my mouse went over the window, giving the cool effect that the frozen target was still alive, detecting my efforts in real time. So what to do now?
- checked windbg on another machine, then olly - all tests exhibit same behavior
- compared PEB and TIB before and after the protection looking for some magical flag setting crap that the target may be doing.... no big differences
- the target loads drivers, so fearing some rootkit behavior, compared nt!KiTrap03 before and after the protection, no changes
- continuing this way, compared nt!CommonDispatchException and then nt!KiDispatchException, still no differences
- using the leaked Windows 2000 source (from torrent), omeg's fine comments on KiDispatchException (http://omeg.pl/code/XP_32_KiDispatchException.txt) and ReactOS (http://doxygen.reactos.org/blah/blah) it was easy to create an annotated IDA listing of my particular ontkrnlpa.exe
- traced the difference to a call to nt!DbgkForwardException which would return 0 during the protection - tracing is a little complicated by the way: KiDispatchException is part of the logic path that eventually communicates with KD itself - it splits into two paths several times depending on whether the exception came from user or kernel mode - obviously you can only use KD (insert BP, single-step) on the user mode paths otherwise the CPU will loop, interrupting on the same BP continuously
- tracing into this, found this crap:
nt!DbgkForwardException+0x2b: 80639e31 64a124010000 mov eax,dword ptr fs:[00000124h] 80639e37 f6804802000004 test byte ptr [eax+248h],4 80639e3e 7404 je nt!DbgkForwardException+0x3e (80639e44) ; success 80639e40 33c0 xor eax,eax ; zero return value, indicating failure
this value was 4 during the protection, so the je/jz was skipped and the failure path taken - patching this in memory allowed breakpoints and stepping to happen!
- so wtf is this check? ReactOS again is indispensible, with its code for DbgkForwardException - didn't take much to match this up:
00338 /* Check if this is to be sent on the debug port */ 00339 if (DebugPort) 00340 { 00341 /* Use the debug port, unless the thread is being hidden */ 00342 Port = PsGetCurrentThread()->HideFromDebugger ? 00343 NULL : Process->DebugPort; 00344 } - finally, googled for this HideFromDebugger and found ivanlef0u's page (http://www.ivanlef0u.tuxfamily.org/?p=48) where he explains this protection completely over 3 years ago! man am I behind!
Oct 22, 2010 EDIT: upb sent me this rootkit.com link dating back to 2005 so this may not be news to anybody
2010-08-13
Shmoocon 2010 Crypto Pack Solved! And Hidden Monomials!

So Shmoocon 2010 challenge pack finally has a published solution! See numernia's solution here where he used MAGMA's Grobner basis facilities and jB's keygen source here where he never mentioned how the parameters of the keygen were arrived at. Of the five challenges only crypto4, the "taste of post-quantum" binary, had something new in it.
The equations you see are the most explicit way to represent MQ system (no lookup table or other type of "compression" was used as in gbe32241's work). See the HFE challenge here for a very similar setup.
I think the start of all these schemes was the MI C* scheme (see paper "Public Quadratic Polynomial-Tuples For Efficient Signature-Verification and Message-Encryption" by Matsumoto and Imai). The best explanation I've found though is probably in Koblitz's Algebraic Aspects of Cryptography.
So the main idea is that you can compute certain exponentiations in an extension field in an alternative way. First you treat the extension field elements as a vector space over the base field. This vector space has many basis to choose from, and any element can also be represented in terms of any chosen basis (the canonical one works just fine). Carefully chosen exponents of these elements resolve to linear transformations and linear expressions of the vectors. And the product of two of these special exponents resolves to a quadratic system of equation. I gave clue "Remember that an extension field is a vector space over its ground field."
The MI scheme and schemes to follow (HFE and so-on) do their best to hide this exponentiation by wrapping the expression for the exponentiation in linear transformations or adding/removing variables and equations. It's these obfuscating elements that become the private information. You didn't have to worry about any of this due to the clue: "there is no scheme in the system, no trapdoor".
So how to solve this thing? Let's treat the system like a black box. If you suspect that the black box is performing exponentiation, what's the simplest test to affirm this? Send in the identity: {1}. No matter the exponent, the identity will be returned. In the polynomial basis representation of the elements, we still don't know which direction the coefficients are listed though. No problem. With a 40-bit input, we try a 1 coefficient at either end:
blackbox(0x8000000000); // returns 000000E0BCE7BA8A blackbox(0x0000000001); // returns 0000000000000001Cool so now we know the LSB of the input is the 0'th coefficient, and it is easy to send in {1}, {x}, {x+1}, etc. But we are faced with a new problem: we don't know what reduction polynomial is used in the field computations. There is only one GF(2^40) field, but the same elements have drastically different representations depending on the reducing polynomial (math nerds talk about isomorphism here).
Can we craft some probe inputs so that the black box will yield to us its reduction polynomial? Yes!
We send element {x}. The blackbox will give us {x}^e (mod p) where e is the unknown exponent and p is the unknown reduction polynomial. We send also element {x^2} and the blackbox will return to us {x^2}^e (mod p) = {x}^(2e) (mod p).
Both of these results are already reduced (mod p). But *OUTSIDE* of the blackbox, we square the first result ourselves on the left hand side, and equate to the second result on the right hand side:
({x}^e (mod p))^2 = {x}^(2e) (mod p)
-> p | ({x}^e (mod p))^2 - {x}^(2e)
-> p * q = ({x}^e (mod p))^2 - {x}^(2e)And q is just some other polynomial. So we compute the right hand side of this last equation and factor it, hoping to find some large 40-degree irreducible polynomial! Enough talk, let's do it!blackbox(0x0000000002 /* {x} */); // returns 0x0EFFD5DBF6 which is {x^n}
blackbox(0x0000000004 /* {x^2} */); // returns 0x0400040008 which is {x^(2n)}Let's flee to our CAS now, the venerable PARI/GP! We convert these results to polynomials a, b:a = (x^35 + x^34 + x^33 + x^31 + x^30 + x^29 + x^28 + x^27 + x^26 + x^25 + x^24 + x^23 + \
x^22 + x^20 + x^18 + x^16 + x^15 + x^14 + x^12 + x^11 + x^9 + x^8 + x^7 + x^6 + \
x^5 + x^4 + x^2 + x)*Mod(1,2)
b = (x^34 + x^18 + x^3)*Mod(1,2)And finally reveal our p!lift(factor(a*a + b)) [x 2] [x^2 + x + 1 1] [x^12 + x^9 + x^5 + x^4 + x^2 + x + 1 1] [x^14 + x^13 + x^11 + x^10 + x^7 + x^6 + x^3 + x + 1 1] [x^40 + x^38 + x^37 + x^36 + x^35 + x^33 + x^30 + x^29 + x^27 + x^26 + x^24 + x^23 + x^22 + \ x^19 + x^15 + x^14 + x^12 + x^11 + x^6 + x^5 + 1 1]It is the last 40-degree polynomial, converted to bit representation, it's 0x017A6DC8D861.
Finding the exponent e is simple now: you may brute outright, brute only exponents that are coprime with ord(GF*(2^40)) (else the blackbox is not a bijection), or use Coppersmith or whatever your CAS uses. It's low, just 257.
So the blackbox is doing exponentiation by 257 and field elements are represented bit-wise with the discovered polynomial. To invert, just exponentiate by d = 257^-1 (mod ord(GF*(2^40))) = 551894941568.
2010-05-29
Conjan's "Jump Around"

The serial verification function's instructions are reordered and linked with unconditional jumps. The solution shows how to disassemble the code into a linked list of instructions, remove the jumps, and recover the original code.
2010-05-14
SEH Checklist
- seh node must be on stack (thanks JPassing.com)
- seh handler must be on non-stack (thanks JPassing.com)
- seh handler nodes must appear in-order on the stack (imagine deeper functions' frames going up the stack, towards lower (less quantity) addresses) (thanks roxfan and Clandestiny post on woodmann)
- seh handler must exist in safeseh list (if it exists, see IMAGE_LOAD_CONFIG_DIRECTORY.SEHandlerTable which is the IMAGE_DIRECTORY_ENTRY_LOAD_CONFIG directory entry in IMAGE_OPTIONAL_HANDLER)
- handler addresses in the safeseh list must be sorted ascending
- IMAGE_OPTIONAL_HEADER.DllCharacteristics must not have flag set IMAGE_DLLCHARACTERISTICS_NO_SEH (this is set by default for Visual Studio when compiling with /SafeSEH:no and no other handlers present (yes even for exe's) ...caught by RtlCaptureImageExceptionValues() WARNING: LET ME RETRACT THIS, NOT ALWAYS)
As Ivanlef0u commented, analysis of RtlIsValidHandler() itself trumps any type of listing we could possibly do. Check his links:
- http://www.eeye.com/html/resources/newsletters/vice/VI20060830.html
- http://sf-freedom.blogspot.com/2007/07/ms07-029-series-part-2-exploiting-dns.html
2010-03-28
Neotren's CryptoME

Your registration data is RSA decrypted, then checked for signature (DLP type). But the signature check uses the same modulus as in the RSA decryption part, giving you a clue to the existence of a subgroup, and the generator of that group. The exponent is capped at 7 bytes, making it possible to search cleverly within this range. Once the subgroup is found, a factor is revealed (and thus the other also). This is a long standing unsolved crackme on crackmes.de and unfortunately neotren had to clue us to the p-1 factoring algorithm, dropping the difficulty significantly.
Lately I read an article about how this one particular C64 user manual had nearly every detail of how the entire machine worked (insane depth compared to manuals of today) and then just a few days ago I read an announcement where the C64 is being re-released. I kind of want one of the classic machines for some reason :) And now this cool emulated game.
2010-03-17
MR.HAANDI's "Intersection #1.0"
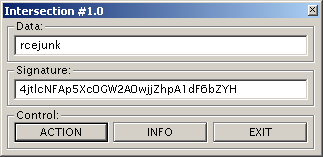
It's compiled against NTL and *alot* of code has to be sifted through to understand what is going on. It's a custom scheme:
To solve it, you need to express the PointB in terms of PointA multiplied by some coefficient k (solving the DLP). This can be done by finding the curve order (#E) and tracing the provided name/serial. But the DLP discovered here is inflated for this particular name/serial. After discovering how "close" PointA and PointB are in a subgroup, it can be reduced to its real value.
Now a cubic equation arises because of the serial's exponent. The equation is reduced mod #E, which is composite. So it doesn't always have solutions. But you can produce many variations of the equation (one which hopefully DOES have a solution) by carefully tweaking the coefficient on the X^0 term.
All crackme calculations are done using curves in the Jacobian intersection form, see:
http://en.wikipedia.org/wiki/Jacobian_curve
http://www.hyperelliptic.org/EFD/g1p/auto-jintersect.html
It was a real IRL killer. Equivalently, a great crackme :)
2010-02-09
Shmoocon 2010 Crypto Challenge Pack
2010-02-08
Really slick way to calculate x % (2^32-1)
mul dword ptr ds:[40120C]
add eax, edx
adc eax, 0
The result is that eax = (eax * [40120C]) % (2^32-1)... Can you prove why?
2010-02-06
Chinese CRC In Operation Aurora
CRC lookup tables normally store a precomputed value for each byte, and thus their tables have 256 entries. This one has only 16, how? If you look closely, the temporary value used to hold the result of the current division is shifted by 4, not 8. Division is done twice. What is going on?
This code is using a nibble lookup table. Two nibbles per byte processed. This optimization has decreased the size of the table by a factor of 16, but only decreased the code speed by a factor of 2, a very cool trade off!
Also notice the direction of the shift, this implementation treats higher significance bits as higher order terms (unlike the typical crc-32, which does the opposite). You can thus find all coefficients except a_16 of the divider polynomial at entry 0x01 (instead of 0x80 in the crc-32 ordering). The polynomial is 0x1021 representing x^16 + x^12 + x^5 + 1. (The a_16 * x^16 term is implicit). The wikipedia page calls this CRC-16-CCITT.
With a little care, we can recreate how this nibble lookup table was generated:
WORD table[16];
for(INT i=0; i<16; ++i) {
WORD crc = i<<12;
for(INT j=0; j<4; ++j) { // for each of 4 possible nibble terms
if(crc & 0x8000) { // high order term present?
crc <<= 1; // term=0 (by implied x^16 divider term)
crc ^= 0x1021; // subtract rest of poly
}
else
crc <<= 1;
}
table[i] = crc;
}
When more spare time arrives, I'll adapt a crc-32 implementation to use this trick! Also add it to your bag of tricks to be on the lookout for when reversing!
Feb 09th, 2010 EDIT: check out the current file archive for the source to an adapted crc-32! It was more difficult than expected to get it to work!
2010-01-27
Numernia's "Keygenme Tre"
Check out Numernia's new crackme at http://crackmes.de/users/numernia/keygenme_tre/!
Probably a little more difficult than 4, but totally possible! Good luck!
2010-01-07
gbe32241's SDDecoder
NNE92-NS62P-TZ9QC-NGEII-6UJ4V (id: 0xDDDD)
PMOFN-WJIJW-DQ9T9-IOM62-RXIIR (id: 0xBBBB)
FGU6J-WAHFJ-T6ZD7-CBKOQ-6LJHD (id: 0x9999)
JT2CQ-6HY7O-6B3DJ-HIAJC-BEC2Q (id: 0x5678)
My attack should work in general for any overlapping s-box scheme. The first implementation was made against SDD64 (the very reason SDD64 was written!) and can generate every possible key for an arbitrary ID. While converting this to 128-bit, I made some error because some id's for the real SDDecoder won't solve, and without the private info, it's difficult to trace why.
It took about 2 single-machine days to extract the private data needed from the public key, and each key generation takes a few minutes (the ones that succeed). When the keygen is debugged I'll submit a solution.
Jan 13th, 2010 EDIT: Solution uploaded! SDDecoder JR v2 falls even better to this same attack, so I downgraded the difficulty to 2... I'm off now exploring other MQ stuff (original C*, HFE, Oil and Vinegar, etc.) Some bonus keys:
HSCTZ-KL9E2-OW67U-UBVEN-VYW7X
PMAUJ-9CJ2W-3SBSY-3A26Y-HAR4V
Z4ANL-MTVRL-3XVL3-A3NMB-3UI39
U3Z3Y-UM337-ZPT9R-4RCKP-C7MSP
SE2FI-B2LOS-EN4LK-HLJ9I-CWZ47
PGPPP-ZVPJW-UEE2Q-FWLY3-3KPPX
Jan 27th, 2010 EDIT: Not challenged enough? See how SDDecoder (DRegZ) was built, and try JRegZ and QRegZ at http://www.webalice.it/giuliano.bertoletti/lca.html.
2009-12-22
death's "Saddam Crackme"
 After being des-decrypted (key derived from GetVolumeInformation()), your serial is used to unscramble an array of function pointers which are critical to the protected application (a cool desktop switcher prog called Smirk).
After being des-decrypted (key derived from GetVolumeInformation()), your serial is used to unscramble an array of function pointers which are critical to the protected application (a cool desktop switcher prog called Smirk).To solve it, you can make a a small number of guesses (relative to the entire size of the table) at proper locations of function pointers within the table, and then search which serials yield arrangements that fit your guess.
2009-12-08
SDD64
r[0] = x[0]*x[0] ^ x[2]*x[0] ^ x[3]*x[0] ^ x[3]*x[2] ^ x[3]*x[3] ^ x[4]*x[4] ^ x[5]*x[2] r[1] = x[2]*x[1] ^ x[3]*x[0] ^ x[3]*x[1] ^ x[3]*x[3] ^ x[4]*x[1] ^ x[4]*x[2] ^ x[5]*x[3] r[2] = x[1]*x[0] ^ x[1]*x[1] ^ x[2]*x[0] ^ x[2]*x[2] ^ x[3]*x[0] ^ x[3]*x[2] ^ x[4]*x[0] r[3] = x[2]*x[0] ^ x[2]*x[1] ^ x[3]*x[0] ^ x[3]*x[1] ^ x[3]*x[3] ^ x[4]*x[1] ^ x[4]*x[2] r[4] = x[1]*x[1] ^ x[2]*x[0] ^ x[2]*x[1] ^ x[3]*x[0] ^ x[3]*x[1] ^ x[3]*x[2] ^ x[4]*x[0] r[5] = x[2]*x[0] ^ x[2]*x[2] ^ x[3]*x[2] ^ x[3]*x[3] ^ x[4]*x[1] ^ x[4]*x[2] ^ x[4]*x[3] r[6] = x[0]*x[0] ^ x[1]*x[0] ^ x[2]*x[1] ^ x[2]*x[2] ^ x[3]*x[0] ^ x[3]*x[1] ^ x[3]*x[2] r[7] = x[0]*x[0] ^ x[2]*x[1] ^ x[3]*x[0] ^ x[3]*x[2] ^ x[4]*x[0] ^ x[4]*x[2] ^ x[5]*x[0] r[8] = x[1]*x[0] ^ x[1]*x[1] ^ x[2]*x[1] ^ x[2]*x[2] ^ x[3]*x[2] ^ x[3]*x[3] ^ x[4]*x[0] r[9] = x[1]*x[0] ^ x[1]*x[1] ^ x[2]*x[1] ^ x[3]*x[0] ^ x[3]*x[3] ^ x[4]*x[0] ^ x[4]*x[1] WHAT: SDD64 This is a 64-bit bit version of Giuliano Bertoletti's DRegZ/SDDecoder license scheme. No code lifted! References: "Asymmetric Cryptography with S-Boxes" - Jacques Patarin "Algorithm for license codes" - Giuliano's sci.crypt post "License Code Algorithms" - Giuliano's website: http://www.webalice.it/giuliano.bertoletti/lca.html "SDDecoder" - crackmes.de andrewl dec07_2009 - first release http://andrewl.brainstemprojects.com HOW: Use sdd64.cpp to generate a random keypair, which are output into public_key.h and private_key.h. Use encoder.cpp with private_key.h to make valid licenses. Use decoder.cpp with public_key.h check license validity. encoder takes as input the license id (decimal format 20-bit integer) and emits an encoded license decoder takes as input an encoded license (hexadecimal format 64-bit integer) and emits "pass" or "fail" message COMPILATION: Written/tested with Visual Studio 9.0 express. With VC6, much wincrypt stuff is not found (HCRYPTPROV, PROV_RSA_FULL, etc. not defined). It can be made to work with VC6, but I do not have time. Compile sdd64.cpp alone. Execution of sdd64 produces public_key.h and private_key.h. Compile encoder.cpp + private_key.h. Compile decoder.cpp + public_key.h. Example command line: cl sdd64.cpp /link advapi32.lib sdd64.exe cl encoder.cpp cl decoder.cpp WHERE: Browse my website for the currently updated file archive and text search for "sdd64". An early version of the software is also included with the SDDecoder Jr. v2 crackme on http://crackmes.de.
2009-11-12
death's "electric-camel"
It does some sha/tiger/blowfish which has to produce the right el-gamal private key to decrypt the goodboy message. See solution and keygen for details. The hardest thing about this crackme is the message of c++ code that goes along with crypto++ library. There's just so much code. I downloaded an old compiler and service pack in order to build the two versions of crypto++ that straddle the 2001 time that this crackme was made, and produced IDA signatures from these.
One of the coolest thing to be learned from this crackme is just how fast MAGMA can solve the DLP for this crackme:
P: cc7346a8b4ffb3f2393b
G: 00000000000000000003
Y: 3e2cb006ad3961beda9d
I left alpertron on overnight and it had not found anything... About 17 hours of computation was continuing when Dcoder from EFNET #cryptography helped me his script:
p := 965489229592273293031739;
K := GF(p);
g := K ! 3;
y := K ! 293611062693023723739805;
x := Log(g, y);
x;
It finds x=0792A1952223 in about .3 seconds!
2009-11-03
upb's "Keygenme Sheg"
Your serial number encodes instructions for a stack-based machine that has instructions for AND, XOR, and PUSH.
The VM is called 16 times and the output must match some values calculated from your username.
This is extremely similar to Malfunction's "Digital Arithmetic" (which came later). In DA, your serial encoded a circuit of NAND gates, and it was shown that NAND gates can be used to make any circuit. In sheg, you have a stack machine, so it is a little harder to produce a functioning "circuit" (the binary operations can ONLY use the two values at the top of the stack, and can ONLY put a result at the top of the stack). Since NOT(x)=XOR(x,1), we get can combine with AND to get NAND, and thus we get anything.
EDIT: upb has informed me that his machine is evaluating a Zhegalkin polynomial, which is neat view of a logic circuit as a polynomial over GF(2).
2009-10-08
Amenesia's "Howl"
Contains a block cipher utilizing finite field arithmetic. You can invert it by reversing the operations and inverting certain field operations. Your serial must encrypt to some values generated from the name and Allen Ginsberg's poem "Howl" (what is an angelheaded hipster anyways!?).
Check out the code for some real calculation of multiplicative inverses in the field using the Euclidean algorithm (no bruteforcing this time!!)
2009-09-28
so61pi's "Keygenme#1"
2009-09-25
Numernia's "Keygenme Tvaa"
2009-09-13
Encrypto's "Aurora"
"SDDecoder Junior"
In this knock-off, the strengthening factors are removed, namely:
- the input and output transforms are separated from the core function
- the key size is reduced from 128 bits to 64 bits
- some other minor simplifications
Here is a list of example codes.
0B9406A6A5CF8D68
7C2E3DC7A9357094
04FEB466BEDCDB92
21E55E6A6B309F70
A8FAC8E4DF56C998
D597329D34D0ED3A
33D0A0EA1092124B
28AC66DD28697C52
1E380939AF1BF545
4FC1636FB7EEAFB0
93B2C52E2B77BD8F
Can you keygen the rest?
UPDATE: (Oct05_2009) a mysterious visitor "z1hye" registered October 5th, 2009 and immediately posted the serial "F365E2149BEA87F1" with ID 0xDEAD!!
UPDATE: (Nov25_2009): Numernia has keygenned it!! check his site or my file archive for sources...going to increase the difficulty towards the real sddecoder now by applying just an input transformation and just an output transformation (but not both simultaneously) ...watch crackmes.de soon
2009-08-04
"Capriccio"
I don't want to give away too much yet. The routine is very small. So hopefully very little time reversing and more time keygenning.
EDIT: so it wasn't as hard as I thought! Villani killed it without even knowing the underlying scheme (which, to me, is even more impressive). Artif owned it up also with ease :) Both solutions posted, thanks guys.
2009-07-14
ZeroCoder's "CrackMe v10.0"
I'm 14 again ruining any chance of being awake tomorrow at school due to a VX zine that I'm nowhere near comprehending. The 16-bit world lives on with ZeroCoder's 425 bytes of frustration that he calls his v10.0 crackme.
It sets up an int1 handler and uses pushf/popf to set the TF. A simple NOP invokes the handler which retrieves "instructions" from an area in the crackme and executes them. Yea it's like a VM, but there are only four instructions. Pretty damn cool so far.
Enter the pain. A simple hash calculation involving add/xor is used with inputs and outputs all over the place (from the crackme, from a supplied password, from the calculations of previous hashes, to the goodboy message, to temporary areas). You don't know what the goodboy is, what characters are in the goodboy or the password, or even what the length of the password is (except that it's capped at 10).
Anyways, it is solvable, although with a little brute-force and guesswork. Like many before it, I could never admit how much time was spent on this thing :P
SIDE NOTES: It was pretty cool using debug.exe and recognizing some of its influence in WinDBG. For a cool description of why interleaving add/xor is so powerful, check out the paper "Block Ciphers and Cryptanalysis" by Fauzan Mirza.
2009-07-06
WinDBG Extension to Read BigLib Numbers
.text:004016B0 push dword_4047A1 <-- arg3
.text:004016B6 push dword_404789 <-- arg2
.text:004016BC push dword_404799 <-- arg1
.text:004016C2 push dword_40478D <-- arg0
.text:004016C8 mov eax, 1
.text:004016CD call sub_4017F3
Even without knowing what sub_4017F3 is, the input/output can be monitored. Load up the extension so that we can view the numbers:
0:000> !load bn
extension: initializing...
0:000> !bn poi(esp)
bignum @00AC0000
00003652B36A37B0C7ECE042
0:000> !bn poi(esp+4)
bignum @00AF0000
00000002
0:000> !bn poi(esp+8)
bignum @009B0000
0000CBEC5F1F97FB14C803CB
0:000> !bn poi(esp+c)
bignum @00B10000
0
Proceed over the call, and check the numbers again:
0:000> p
0:000> !bn 00AC0000
bignum @00AC0000
00003652B36A37B0C7ECE042
0:000> !bn 00AF0000
bignum @00AF0000
00000002
0:000> !bn 009B0000
bignum @009B0000
0000CBEC5F1F97FB14C803CB
0:000> !bn 00B10000
bignum @00B10000
00006F18441B1396928838B5
All the arguments except arg3 remained the same. With some intuition and a verifying test in BigCalto, we see that arg3 = arg0 ^ arg1 (mod arg2) and identify this function as _BigPowMod().
I purposely did some things to encourage rapid re-purposement of the source code: all the code is in one file, there is minimal bloat (just some placeholders with prints where extended functionality can exist), and it compiles with a simple batch file which invokes the Visual Studio command line tools. No project or solution bullshit.
2009-07-04
dihux's Keygenme nr. 2
2009-06-23
upb's Push-The-Pusher
Your name is used to generate an input buffer. Your serial decides which bits of the input buffer are complemented. Finally, the CRC32 of the input buffer must equal a predefined value (0xFAF3CCCE).
Though CRC is so old and there are numerous resources online about its many variations, this turned out to be much much harder than I expected. Here is the final technique:
- find what 32-bit input has CRC32 of 0xFAF3CCCE (brute all 32-bit values or try to work backwards with the long division)
- calculate CRC32 of the input buffer less 32-bits
- since CRC32(input,4,X) == CRC32(input^X,4,0) we can concatenate the four bytes discovered from step 1 to the buffer after having xor'd them by the result from step 2
- the CRC32 of the full input buffer now is 0xFAF3CCCE
If you're facing a similar task, the solution text includes a hand-worked example of CRC32. Oh! And a challenge to you: given a CRC lookup table, how can you quickly find which polynomial was used to generate it?
2009-06-05
Waganono's WagaTemplate

Hehe yet another strange crackme by this guy. This one comes with the about-box template (which has cool fractal animation worth checking out).
The serial verification makes use of just 5 mmx/sse/simd/whatever instructions (I always ignore these strange things!) After some time on google, it is very easy to solve.
What is NOT so easy is getting the floating point crap right. The easiest path is to use your debugger to write the values into the xmmX register and then read the register as raw bytes, but not so fast. WinDBG is shown to have MANY bugs when it comes to this.
First of all, the register command and register window will show two different values:
3.60134e-043 7.9881e-041 6.16406e-039 1.71607e-038 <-- from "r xmm1" 3.601337e-043: 7.988102e-041: 6.164064e-039: 1.716068e-038 <-- from register windowAnd evidently, it's not just a rounding issue. Second, if you double click in the register window on this xmm1 value, when you click away, the first float will be set to 0! This is the same for any xmmX register. If you do it to the same register twice in a row, all the floats will be set to 0! WTF? Third, the input into the xmmX register "r xmm0=
2009-05-27
HappyTown's CrackME_0009
2009-05-25
HappyTown's CrackME_0030
This crackme made me read the "quadratic residue" Wikipedia page AGAIN. One day I might have it memorized :)
You end up having to solve:
C*X^2 + Y^2 = U (mod N)
Where C is constant, U is a number derived from your username, and N is the product of two large primes P and Q. The X and Y are the components of the serial.
First you can randomly produce values for either X^2 or Y^2 and solve for the other. Whatever values you use, you must make sure that they're truly squares (mod N) [thus squares both (mod P) and (mod Q)] using Euler's criterion. Luckily, both P and Q are congruent 3 (mod 4) so we get the easy path in deriving X and Y.
But not so fast! Like "D-Racinez Moi" from decades past, solving for either X or Y must be done in pieces, as the modulus is composite, (one piece for P and one piece for Q). You'll have two answers:
X = <something> (mod P)
X = <something> (mod Q)
As primes, GCD(P,Q) = 1, and that means the Chinese remainder theorem will be making a guest appearance as the final step in generating keys.
Also, author notes that "Public Key algorithm INSIDE." - does anybody recognize this algorithm?
2009-05-05
HappyTown's CrackME_0026

The moderator comments revealed that it did some type of ECC, so I had to try it in continuation of my elliptic journey. Fortunately, it implements ECDSA just like WiteG #10. But in this crackme, you have to actually forge a signature for a message generated from your user name (actually it is bignum(sha1(user)) just like the previous crackme!).
Of course ECDSA would be useless if forgery were possible without knowing the private key. I enlisted Mr. Haandi's ECDLP Solver v0.2a to find the discrete log (just the scalar k so that k * G = public key). The crackme uses extremely small parameters for its curve, so the solver finished in about 1/5th of a second.
From there it's just calculation...
2009-05-04
WiteG #10: What do you think you know about signatures?
The idea of this crackme is a challenge: to generate a single ECDSA signature for two different messages (computed from the username). The cracker gets free choice of the public key QA and the randomized parameter k.
Two messages, one signature? It's impossible right?
Well after many lonely mornings in front of the glow, it really is possible!
The spoiler is that in the ECDSA signature verification computations, only the x-coordinate of the computed point is checked. For each x-coordinate on a curve over Fp, there are two y-coordinates (two distinct points total, inverses of one another for point arithmetic on the curve). Here is a good example from Certicom's ECC Java applet:
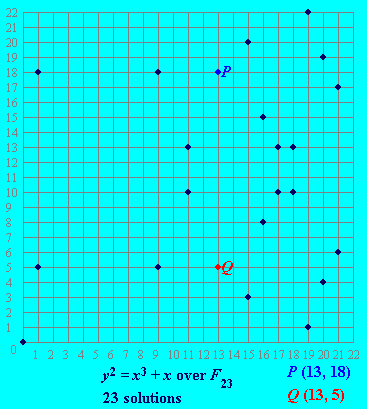
Given some point k*G, where k is an integer and point G is the generator, you don't have to do anything difficult like the ECDLP to find -(k*G). One of the six generators is G=(17,10). Calculating 1*G, 2*G, ... this generator produces:
(17,10), (16,15), (15,03), (09,18), (21,17), (01,18), (11,10), (18,13), (20,04), (13,05), (19,22), (00,00), (19,01), (13,18), (20,19), (18,10), (11,13), (01,05), (21,06), (09,05), (15,20), (16,08), (17,13), (inf)
The inverse points are mirrored around the (0,0) point in the middle of the sequence. We can put this symmetry into a simple formula:
k * G = -((N-k) * G)
Where N is the order of the generator. Like in the above picture, P and Q are inverses. But suppose we didn't know this beforehand, and only knew that P=14*G. We could discover Q by calculating (24-14)*G = 10*G = Q.
Ok so we can find the two inverse points easily in terms of a coefficient and a generator point. Now just try to get the two separate messages to have these two separate points as signatures. See my solution for more detail.
It is mentioned in WiteG's comment that it has been keygenned by jB before, a known keygenning master. If I find the time I will his solution and maybe add some more comments.
2009-04-19
GiveMeMoney by ksc91u
According to Google, ksc91u is a Taiwanese student, and his main study lately is keeping me from getting any sleep trying to keygen his little creation:

His crackme uses Crypto++ library, which is a royal pain to disassemble. I used default settings in the Crypto++ Visual Studio project file to compile the lib and attempt to make an IDA sig, but it only recognized 16 functions in the crackme, and none of them were important names in the serial verification routine. An OpenRCE post here seems to mirror my frustration. Look at this example code for simply calculating a hash here:
#include "sha.h"
#include "base64.h"
std::string digest;
CryptoPP::SHA256 hash; // don't use MD5 anymore. It is considered insecure
// Thank you, Wei Dai, for making this possible:
CryptoPP::StringSource foo("CryptoPP is cool", true,
new CryptoPP::HashFilter(hash,
new CryptoPP::Base64Encoder (
new CryptoPP::StringSink(digest))));
std::cout << digest << std::endl;
"Thank you, Wei Dai, for making this possible"? This is crazy! I want my init(), update(), final() calls, not this object-within-an-object source-pipe-sink paradigm garbage!
There is some help from openrce user igorsk who published his "Microsoft VC++ Reversing Helpers" IDA scripts. Other than that, it's the classic poking around, trying different inputs and watching the output (and verifying against your calculator), and tracing deep :) If you can get through this, the hard part is over.
Your serial encodes a point on an elliptic curve over Fp which is multiplied (point multiplication on the curve) by a constant within the crackme. The resulting point's X coordinate acts as a modulus for which the second part of your serial has its inverse found. From this inverse is derived a decryption key for a DLL which exports the goodboy function.
Fortunately, some valid keys come with this crackme, and the magical inverse value is revealed to be constant simply by tracing through the crackme with a valid key. It is prime, so it will have an inverse mod any number (specifically any X coordinate from any random point on the curve).
Though not having anything to do with the crackme, it is interesting to see the curve used by the crackme over the real numbers and imagining the the group addition law:
gp > E=ellinit([0,0,0,589755319233708863313827,435926913486323829977567]) gp > ploth(X=-.7393,-.7390,real(ellordinate(E,X)))
 If you look near Y=0, it is hard to image a tangent line at a point intersecting the curve in another spot. But then zoom out:
If you look near Y=0, it is hard to image a tangent line at a point intersecting the curve in another spot. But then zoom out:
ploth(X=-1000000000000000000,1000000000000000000,real(ellordinate(E,X)))
 The way that the curve is concave is somewhat convincing that the tangent line would eventually hit it, although it would be lightyears above or below the X axis. I would really like to learn how to graph the points of the curve over Fp.
The way that the curve is concave is somewhat convincing that the tangent line would eventually hit it, although it would be lightyears above or below the X axis. I would really like to learn how to graph the points of the curve over Fp.
2009-04-09
Locating the code that executes upon a button press
SetWindowsHookEx() lets a callback be notified of different events. When supplied WH_CALLWNDPROC it can be notified of messages before they go to the windows procedure. Moreover, the lParam you are sent is a CWPSTRUCT* which has a handle to the destination window. This can be given to GetWindowLongPtr() with GWL_WNDPROC to find what code gets called.
I know spy++ type tools do this type of thing already, but it was a learning experience to make a tool. It does exactly what is described above. Just give it a PID and it will enumerate all threads and install the monitoring hook. It actually injects a DLL which opens a pipe back to the control program to send it the caught messages:

Instead of complicating it with filters and stuff, just grep the output to capture what message you are looking for. For instance: msgspy.exe 924 | grep 111 to get your WM_COMMAND. Download this tool msgspy_v1.rar in filedump.
Many times the PROC given for the command will be some default function in user32 or comctl32 or something (eg: COMCTL32!Button_WndProc). In this case you can trace through until the code in your target is hit or use your debuggers facility to do this, if it exists (go to user code in Olly).
One difficulty in making this tool was that it would often return values like 0xFFFFF052 for the WndProc. On the MSDN page for CallWindowProc the strangeness is explained, "If this value is obtained by calling the GetWindowLong function with the nIndex parameter set to GWL_WNDPROC or DWL_DLGPROC, it is actually either the address of a window or dialog box procedure, or a special internal value meaningful only to CallWindowProc."
That sucks - this internal magic token is useless to us trying to find the code. I traced into user32!CallWindowProc to see what it did with these funny values. My CallWindowProc is actually typedef'd to CallWindowProcA. This calls CallWindowProcAorW which performs this test:
.text:7E429FD3 mov eax, 0FFFF0000h .text:7E429FD8 mov ecx, esi <-- WndProc .text:7E429FDA and ecx, eax .text:7E429FDC cmp ecx, eax .text:7E429FDE push edi .text:7E429FDF mov edi, [ebp+arg_8] .text:7E429FE2 jz special_valueSo what makes the specialty of these WndProc's is that their top 16 bits are set. Immediately into special_value, we get:
.text:7E42A99C mov dl, 7 .text:7E42A99E mov ecx, esi <-- WndProc .text:7E42A9A0 call HMValidateHandleNoRipThis HMValidateHandleNoRip function is way beyond me: it does some system call crap to get a struct in ebx and blah blah who cares. But what does with the return value is treats it like some type of structure and extracts the member 24 bytes inwards:
.text:7E42A9C6 mov esi, [eax+18h]And this is the real function pointer. The only way I could think of to get this feature in my code was to scan user32 for the function HMValidateHandleNoRip, having made a signature that consists of just the opcode (the operands are like wildcards). This blows because if user32 ever looks different (different service pack, different windows version?), the tool will need to fall back and only display the special tokens, unable to resolve them. Have a better idea? Please comment. Anyways so if it is found (which it does on my XP SP3 machine), it can be used to resolve the special tokens just fine.
typedef struct HMVALIDATESTRUCT
{
// filler to get to offset 0x18
UINT a, b, c, d, e, f;
UINT fptr;
} HMVALIDATESTRUCT, *PHMVALIDATESTRUCT;
typedef PHMVALIDATESTRUCT (__fastcall *PFN_HMVALIDATEHANDLENORIP)(WNDPROC, BYTE);
PFN_HMVALIDATEHANDLENORIP ValidateHandle = ScanForFunction(hUser32);
WndProc proc = GetWindowLongPtr(pcwp->hwnd, GWL_WNDPROC);
PHMVALIDATESTRUCT foo = ValidateHandle((WNDPROC) proc, 7);
spymsg.wndProc = foo->fptr;
Ugly but it works!
You may find this tool useful for delphi apps or other programs made with workshop type development environments. A recent example I used it on is obnoxious's AutoIt crackme.
May 11th, 2009 EDIT: zip now includes source!
2009-04-03
DoomsDay's ReverseMe - FindThePassword v1
 A nice console crackme with spinning slash at only 4k! :)
A nice console crackme with spinning slash at only 4k! :)The main idea is to reverse addition and squaring (composed of additions) that are implemented using just bit operations. It is pretty difficult.
EDIT: DoomsDay was kind enough to share his source code! see DoomsDay_FindThePassword_v1.asm in crackmes
2009-03-20
Eggi's Arteam Crackme #1

This was recently posted to crackmes.de. It is another crackme where your serial is used to decrypt some code that will eventually execute.
Specifically here, a word is made by summing your serial characters with strlen(serial). This word then is xor'd sequentially (no feedback) across 10 words.
Before execution reached the decrypted code, a one byte comparison is made for validity, revealing half of the xor key.
To get the other half, I used z0mbie's XDE engine on trial decryptions (incrementing trial keys) to see which key produced the most normal disassembly; normal meaning it consisted of typical instructions: push, pop, call, etc.
UPDATE: crackme was removed from crackmes.de since it is preferred that the real author submit - a copy is in this site's crackmes folder
Paltalk Password Storage Algorithm

There are a ton of password recovery tools for this program, so how hard can the storage algorithm be?
Homemade schemes can be very interesting. Here, in the registry is stored one dword for each of the password characters.
The username and is interleaved with the volume serial number. Like "myuser" and volume serial DEADBEEF come to: "mDyEuAsDeBrEEF". That is then trippled: "mDyEuAsDeBrEEFmDyEuAsDeBrEEFmDyEuAsDeBrEEF".
The registry value is then used to subtract values from certain characters, resulting in the password. It is easier to convey in code: see paltalk_pw_recover.cpp in filedump.
2009-03-11
Cyclop's Angler

A fellow mod from crackmes.de has posted an interesting crackme that will exercise your number theory knowledge. It's short and not too hard, have fun!
Funny hint: the color of the crackme may be some clue!
EDIT: freesoul freaking solved it in record time! (I admittedly had a head start as it rested in the moderator queue). So the spoiler is that it's Goldbach's conjecture. The serial has four pairs of numbers that must be prime and sum to four CRC's generated from the username (which are incremented if odd).
Cyclops said that not all usernames have serials, but I think they do. The CRC's are 32-bits, and the conjecture has been tested way up above 2^32. Since the addition check happens in the confines of a 32-bit register, you can even generate serials for when a CRC is 0 or 2 (aim for 2^32 and 2^32+2).
2009-03-07
Internal binary representation of FGInt
// TFGInt = Record
// Sign : TSign;
// Number : Array Of LongWord;
In a crackme, the MD5 of "myname" == ABB45C192F0818FF22B7DDDA8566DAC3 is made into an FGInt via Base256StringToFGInt(). Looking at the memory where this FGInt is stored:
0014fc04 00000001 00862354 0014fc34 0001d4c7
Where 000000001 is the Sign member and 00862354 is the Number member.
00862354 00000009 44414333 706a6c6c 11111104
00862364 119211ba 13846463 48c60706 50cc4e4c
00862374 21211a1a 00000041 00860a3c 0001f604
Where 00000009 is the amount of dwords in the array, and the 44414333 706a6c6c 11111104... are the members of the array.
Strange, but the only quantities contributing to the FGInt are the 31 lower bits of the 9 dwords.
Here is some C where a 64-bit value is used as kind of a bit buffer to shift in the 31-bit chunks. When more than 8 are collected, a byte can be consumed. If you know a better way, please tell me.
typedef struct {
ULONG nLongWords;
ULONG longWords[1];
} DELPHI6ARRAYLONGWORD, *PDELPHI6ARRAYLONGWORD;
// assume DELPHI6ARRAYLONGWORD variable darray and byte buffer bytes[]
for(int i=0; i<darray.nLongWords; ++i)
OutputRaw("digit %d: %08X\n", i, (ULONG)digits[i]);
ULONGLONG ullBuff=0;
UINT bytei=0;
UINT nBitsInBuff=0;
for(int i=0; i<darray.nLongWords; ++i)
{
ullBuff |= (digits[i] << nBitsInBuff);
nBitsInBuff += 31;
while(nBitsInBuff >= 8)
{
bytes[bytei++] = ullBuff & 0xFF;
ullBuff >>= 8;
nBitsInBuff -= 8;
}
}
if(nBitsInBuff)
bytes[bytei++] = ullBuff & 0xFF;
for(int i=bytei-1; i>=0; i--)
OutputRaw("%02X", (ULONG)bytes[i]);
The output is good:
The bytes of the FGInt (within the 31-bit chunks) are stored little-endian. The 414242... start the "ABB..." from the hash.
digit 0: 44414333
digit 1: 706A6C6C
digit 2: 11111104
digit 3: 119211BA
digit 4: 13846463
digit 5: 48C60706
digit 6: 50CC4E4C
digit 7: 21211A1A
digit 8: 00000041
0000004142423434433139304630383038464630324237404444410035363644414333
Feb 02, 2010 EDIT: Numernia informed me that 31-bits is chosen to easily propagate carry bits across addition (carry flag and adc instruction are not accessible from delphi)... a closer look at FGInt source verifies this:
Switch "rest" with "carry" in your mind. 2147483647 is 0x7FFFFFFF.
2009-03-02
Xspider's xCryptokGnMe #1
 This crackme does a few things to distract you, like getting the dialog text of fields that don't exist, computing a SHA1 hash and then not using it, and other calculations. Ultimately 16 calls to blowfish's F() function (that does not use the tables within the blowfish context struct) work on the first 64-bits of your entered username. A little custom math after that computers your 64-bit key. Crackme is fishable.
This crackme does a few things to distract you, like getting the dialog text of fields that don't exist, computing a SHA1 hash and then not using it, and other calculations. Ultimately 16 calls to blowfish's F() function (that does not use the tables within the blowfish context struct) work on the first 64-bits of your entered username. A little custom math after that computers your 64-bit key. Crackme is fishable.
2009-03-01
Trevil's Keygenme #1
Check out Trevil's (a cool guy from #c4n) keygenme. It's old, and does some basic RSA stuff. Just encrypt(user) == serial. But the fact that its in VB made it a little difficult. I probably would have been lost without Googling for some of the strings. See if you can do it without searching!
Malfunction's "Digital Arithmetic"
 This crackme has encrypted functions and to decrypt them, you must trace through some exceptions. Luckily they follow a standard form and a static deprotector can be made (included in the solution.)
This crackme has encrypted functions and to decrypt them, you must trace through some exceptions. Luckily they follow a standard form and a static deprotector can be made (included in the solution.)The functions eventually reads in your key file, which must contain a description of a NAND gate logic circuit whose simulation verifies some calculations made in the crackme from your username. The bits of some generated inputs are the hi/lo inputs of the nand gates, and the output hi/lo is the output bits.
The major weakness is that the crackme only generates ten input/output pairs to verify that your circuit works. For instance the username "malfunction" generates:
input output
0x103473A2E909556A 0xD5C5F13B5D19C47B
0xD58409F7ACE0B636 0xCC00155EACD0443C
0xB8E23CEC3499154F 0xDA1F03994BAD8545
0x7D0D5F4A4B7EE494 0x3700BB945FE19291
0x3C8249E1942D1311 0xB21A80661AF8410E
0x6450E69AC82EF542 0x149E7890D8C07AFC
0xFA754B5BE6241519 0x4D0FF60D1535ED08
0xD2AC47F7A3DDC7F2 0xD8002D85A3D9E8D5
0x67BF14070BAAE972 0x8F000EC07480C934
0x7D173C2B4336EE20 0xE1F3F4387250BC3F
Here again (like in BUBlic's Xor2Zero) the strength of understanding GF(2) and vectors of GF(2) is shown (even if it is basic as hell, like mine :)). The bit columns of the input and outputs can be thought of as vectors. This yields 64 vectors, each with 10 dimensions.
Since the smallest basis of ten dimensions is a set of 10 vectors, having 64 nearly guarantees that we have a basis here. So we must be able to find some vectors that, summed (xor) over GF(2) give us any output vector we want. In reality, it is difficult to find some output vector that needs more than 3 input vectors.
Thus we could solve Digital Arithmetic if only it was a simulation of XOR gates. But it's a simulation of NAND gates. What to do?
XOR(A,B) = NAND(NAND(A,(NAND(A,B)),NAND(B,NAND(A,B)))
2009-02-26
Waganono's D-Vinaigrez Moi

Another one for my Waganono collection :) Your serial number "decrypts" (xor) a ciphered message in the crackme. The crackme verifies proper decryption by using a keyed hash message authentication code. You get a French message and a song as a reward! You can see patterns in the ciphertext that clue you to the length of the key. Next, individual bytes of the key can be toggled to maximize the amount of "normal" text in trial decryptions.
BUBLic's Xor2Zero

This one is really neat! MD5 is used to generate a system of linear equations over GF(2). Your serial encodes a solution to the equations. Only XOR, and AND can be used. A reduced Gauss-Jordan elimination algorithm was employed to make a keygen.
BUBLic's Security^-1

MD5 is used on the username to generate what's called a truncated polynomial within the NTRU cryptosystem. It represents the plaintext. The entered serial number encodes a polynomial that is the ciphertext, and the crackme decrypts it to compare it to the plaintext. Keygenning is just enciphering the the poly produced from the username, but a small shortcut can be taken.
Bruteforceme#1_astigmata
A machine has been dedicated to searching for the key to Bruteforceme#1_astigmata, a crackme which has stood unsolved for quite a while now. (LINK: Bruteforceme#1_astigmata). What's so neat about the crackme is that there are really only four instructions that make it so difficult. Those instructions are iterated 1E8 times. RCR has no 1:1 inverse, but it is invertible. The branching factor, moving backwards, is so large that any attempt to go back more than 100 iterations becomes infeasible. It is also not difficult to find (eax,ebx) pairs that lead to a solution by just allowing the loop to run unbounded, and stopping when the xor result is 0xD5446474 (keep a 1E8 history). So back to brute force. My biggest fear is that no answer exists. I'm confident that the search is correct because I compared some outputs with outputs of the crackme. Some inputs were also chosen, ran them through the crackme to get the xor result, and then the search was tested to see if it could really find the chosen input.

UPDATE! After nearly 9 days of searching, on Christmas eve morning (2008), the serial was found :) See the solution in the crackme solutions download link or on crackmes.de.
JE's "jE!_CRC_DRx"
At only 11k, this crackme is a real pain. It's a puzzle from you must supply an input file that coerces the crackme into displaying a message box (the usual user32!MessageBoxA). There is some anti-debug. The calculation is based on the bytes of the executabe memory image, so it will change if BPX's are present. The code itself has int3 and a handler for int3, making you wonder how much the cme behavior will intersect with your debugger. The DRx registers are used as the area for calculations, an obstacle for BPM. It also depends on the trap flag being set in certain places, so single-stepping is not an easy option. Though I lost alot of time on it, it forced me to learn alot about my debugger (making it pass and handle certain exceptions, tracing SEH, etc.) For some reason, I find jE!'s comments very entertaining:
U must buid KEY-file, which forces cr0ckme to show msgbox: WOW! CONGRATULATIONZ! main cr0ckme idea is playing with SEHs.. (look at comment in code below) after i imagined some fun-way to call MessageBox.. fun is fun, but what for U!? btw, maybe i will call it 'READY-STACK' & write another cr0ckme on this idea! so i mostly removed my-fun! U must discover that fun-way first! (info leaved should be enough.. U need fUntaziE+LogiQ, have U!?) then you need discover main ck0ckme idea.. o-o-o!