MR.HAANDI's "Intersection #1.0"

[difficulty: 8][protection: ECC]






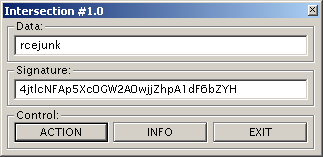
It's compiled against NTL and *alot* of code has to be sifted through to understand what is going on. It's a custom scheme:





To solve it, you need to express the PointB in terms of PointA multiplied by some coefficient k (solving the DLP). This can be done by finding the curve order (#E) and tracing the provided name/serial. But the DLP discovered here is inflated for this particular name/serial. After discovering how "close" PointA and PointB are in a subgroup, it can be reduced to its real value.

Now a cubic equation arises because of the serial's exponent. The equation is reduced mod #E, which is composite. So it doesn't always have solutions. But you can produce many variations of the equation (one which hopefully DOES have a solution) by carefully tweaking the coefficient on the X^0 term.

All crackme calculations are done using curves in the Jacobian intersection form, see:

http://en.wikipedia.org/wiki/Jacobian_curve
http://www.hyperelliptic.org/EFD/g1p/auto-jintersect.html

It was a real IRL killer. Equivalently, a great crackme :)