According to Google, ksc91u is a Taiwanese student, and his main study lately is keeping me from getting any sleep trying to keygen his little creation:

His crackme uses Crypto++ library, which is a royal pain to disassemble. I used default settings in the Crypto++ Visual Studio project file to compile the lib and attempt to make an IDA sig, but it only recognized 16 functions in the crackme, and none of them were important names in the serial verification routine. An OpenRCE post here seems to mirror my frustration. Look at this example code for simply calculating a hash here:
#include "sha.h"
#include "base64.h"
std::string digest;
CryptoPP::SHA256 hash; // don't use MD5 anymore. It is considered insecure
// Thank you, Wei Dai, for making this possible:
CryptoPP::StringSource foo("CryptoPP is cool", true,
new CryptoPP::HashFilter(hash,
new CryptoPP::Base64Encoder (
new CryptoPP::StringSink(digest))));
std::cout << digest << std::endl;
"Thank you, Wei Dai, for making this possible"? This is crazy! I want my init(), update(), final() calls, not this object-within-an-object source-pipe-sink paradigm garbage!
There is some help from openrce user igorsk who published his "Microsoft VC++ Reversing Helpers" IDA scripts. Other than that, it's the classic poking around, trying different inputs and watching the output (and verifying against your calculator), and tracing deep :) If you can get through this, the hard part is over.
Your serial encodes a point on an elliptic curve over Fp which is multiplied (point multiplication on the curve) by a constant within the crackme. The resulting point's X coordinate acts as a modulus for which the second part of your serial has its inverse found. From this inverse is derived a decryption key for a DLL which exports the goodboy function.
Fortunately, some valid keys come with this crackme, and the magical inverse value is revealed to be constant simply by tracing through the crackme with a valid key. It is prime, so it will have an inverse mod any number (specifically any X coordinate from any random point on the curve).
Though not having anything to do with the crackme, it is interesting to see the curve used by the crackme over the real numbers and imagining the the group addition law:
gp > E=ellinit([0,0,0,589755319233708863313827,435926913486323829977567]) gp > ploth(X=-.7393,-.7390,real(ellordinate(E,X)))
 If you look near Y=0, it is hard to image a tangent line at a point intersecting the curve in another spot. But then zoom out:
If you look near Y=0, it is hard to image a tangent line at a point intersecting the curve in another spot. But then zoom out:
ploth(X=-1000000000000000000,1000000000000000000,real(ellordinate(E,X)))
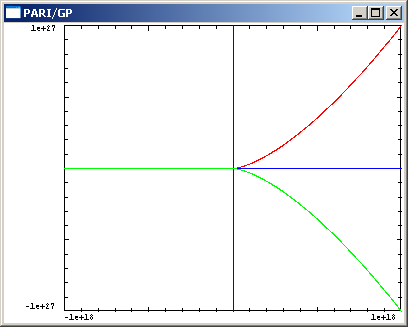 The way that the curve is concave is somewhat convincing that the tangent line would eventually hit it, although it would be lightyears above or below the X axis. I would really like to learn how to graph the points of the curve over Fp.
The way that the curve is concave is somewhat convincing that the tangent line would eventually hit it, although it would be lightyears above or below the X axis. I would really like to learn how to graph the points of the curve over Fp.
very nice ;)
ReplyDeletewelcome to ECC reality :)
artif
More ECC work on the way!
ReplyDeleteI am needing to build an ECC calculator soon too...
Will be helpful for me :)
ReplyDeleteECC != EZ for me :P
When you asked ksc91u about the base point I thought you were going to own up it up :)
ReplyDelete